Opponents of empiricism and science have long asked, “When a human sees things in the real world and spots patterns in the events going on there, then makes statements about what she is spotting, what is doing the spotting? The human mind, and the sense data–processing programs it must already contain to be able to do the tricks empiricists describe, obviously came before any data processing could be done. What is this equipment, and how does it work?” Philosophers of science have had trouble explaining what this mind that does the knowing is, and thus what science, the most rigorous form of knowing, is and is trying to do.

Consider what science is aiming to achieve. What scientists want to discover, come to understand, and then use in creative ways in the real world are what are usually called the “laws of nature”. Scientists do more than simply observe the events in physical reality. They also strive to understand how these events come about and then to express what they understand in general statements about these events, in mathematical formulas, in chemical formulas, in rigorously logical sentences in one of the world’s many languages, or in some other symbol system used by people for conveying their thoughts to other humans. A “natural law” statement must describe one of the ways in which reality works, and, to be considered scientific, the statement must be set down in such a way that it can be tested in the real world.

If claims about this newly discovered real-world truth are going to be worth considering, scientists must be able to test those claims in some real, material way. Thus, any natural law statement that is made, to be of any practical use whatever and to stand any chance of enduring, must first be expressed in some language or symbol system that humans use to communicate ideas with other humans. A theory or model that can be expressed only inside the head of its inventor will die with her or him.

The following is a verbal statement of Newton’s law of universal gravitation: “Any two bodies in the universe attract each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.”

In contrast, the mathematical formula expressing Newton’s law of universal gravitation looks like this:

                                    

And consider another example:

                               

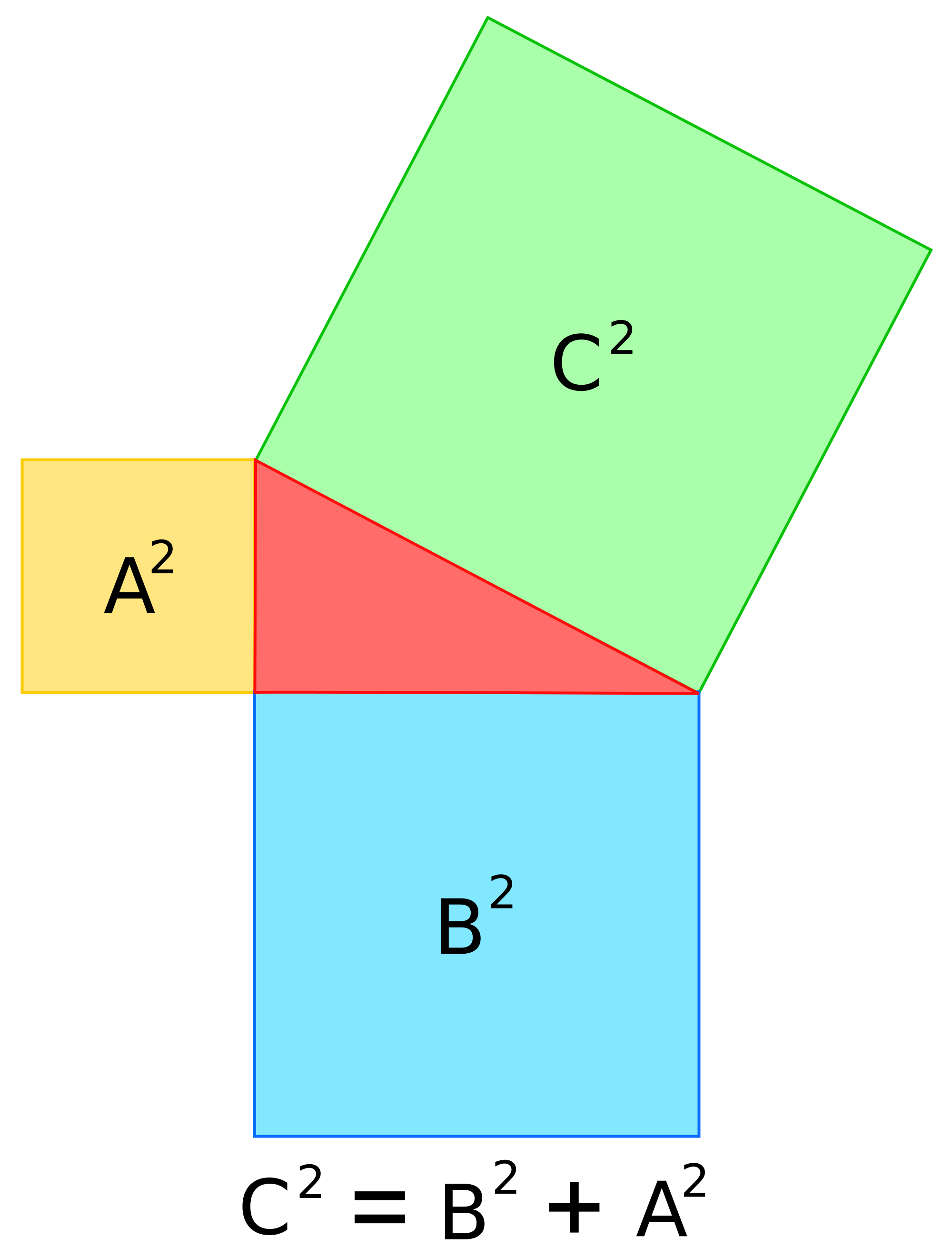
The Pythagorean theorem is a mathematical law, but is it a scientific one? Can it be tested in some absolutely unshakable way in the real world? (Hint: How can you measure the sides and know you’re exactly accurate?) 

 

The big problem occurs when we try to analyze logically just how true statements like Newton’s laws of motion or Darwin’s theory of evolution are. Do statements of these laws express unshakable truths about the real world or are they just temporarily useful ways of roughly describing what appears to be going on in reality – ways that are followed for a few decades while the laws appear to work for scientists, but that then are revised or dropped when new problems they can’t explain are encountered?

Many scientific theories in the last four hundred years have been revised or dropped altogether. Do we dare to say about any scientific law statement that it is true in the unassailable way in which 5 + 7 = 12 is true or the Pythagorean theorem is true?

This debate is a hot one in Philosophy right up to the present time. Many philosophers of Science claim that scientific laws, once supported by enough experimental evidence, can be considered to be true in the same way as valid math theorems are. But there are also many who say the opposite —all scientific law statements are tentative. These people believe that, given time, all such statements get replaced by new statements based on new models or theories.